This is a subpage of Morrison Fleischmann debate to allow detailed study of the paper copied here, from http://lenr-canr.org/acrobat/Fleischmancalorimetra.pdf
The first paper is at ICCF-3. The note at the top of page 1 is a standard addition to papers by lenr-canr.org. As well, the link to youtube on page 18 was obviously supplied later, probably by Jed Rothwell.
However, the debate formally began with the publication in Physics Letters A. It should be kept in mind that Morrison was responding to that, not necessarily the copy below.
page anchors added per lenr-canr copy. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Section anchors:
ABSTRACT [analysis]
General Features of our Calorimetry [analysis]
Modelling of the Calorimeters [analysis]
Methods of Data Evaluation: the Precision and Accuracy of the Heat Transfer Coefficients [analysis]
Applications of Measurements of the Lower Bound Heat Transfer Coefficients to the Investigation of the Pd – D2Ο System [analysis]
A Further Simple Method of Investigating the Thermal Balances for the Cells Operating in the Region of the Boiling Point
CALCULATION
GLOSSARY OF SYMBOLS USED
References
(after each section, as well as above, there is a link to an analysis subpage — once they have been created)
1
The Third International Conference on Cold Fusion. 1992. Nagoya, Japan: Universal Academy
Press, Inc., Tokyo: p. 47.
Calorimetry of the PD-D2O System: from Simplicity via Complications to Simplicity.
Martin FLEISCHMANN, Dept. of Chemistry, Univ. of Southampton, Southampton, U.K.
Stanley PONS, IMRA Europe, Sophia Antipolis, 06560 Valbonne, FRANCE
ABSTRACT
We present here one aspect of our recent research on the calorimetry of the Pd/D2O system
which has been concerned with high rates of specific excess enthalpy generation (> 1kWcm-3) at
temperatures close to (or at) the boiling point of the electrolyte solution. This has led to a
particularly simple method of deriving the rate of excess enthalpy production based on measuring
the times required to boil the cells to dryness, this process being followed by using time-lapse video recordings.
Our use of this simple method as well as our investigations of the results of other research
groups prompts us to present also other simple methods of data analysis which we have used in the preliminary evaluations of these systems.
[analysis]
General Features of our Calorimetry
Our approach to the measurement of excess enthalpy generation in Pd and Pd-alloy
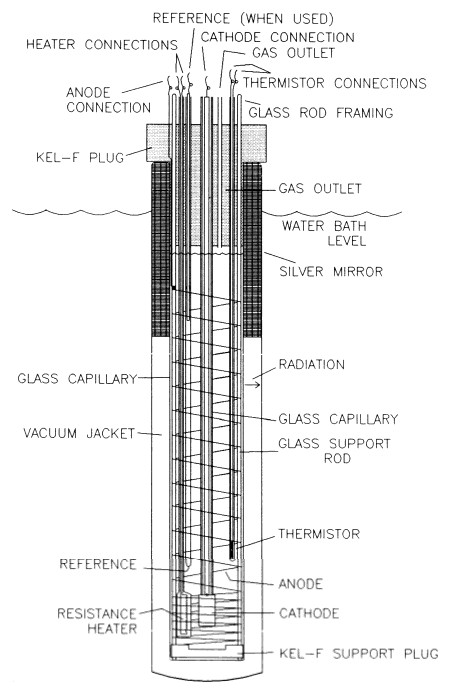
cathodes polarised in D2O solutions has been described in detail elsewhere (see especially (1-5); see also (6)). The form of the calorimeter which we currently use is illustrated in Fig 1. The following features are of particular importance:
(i) at low to intermediate temperatures (say 20-50°C) heat transfer from the cell is dominated by
radiation across the vacuum gap of the lower, unsilvered, portion of the Dewar vessel to the
surrounding water bath (at a cell current of 0.5A and atmospheric pressure of 1 bar, the cooling due to evaporation of D2O reaches 10% of that due to radiation at typically 95-98°C for Dewar cells of the design shown in Fig 1).
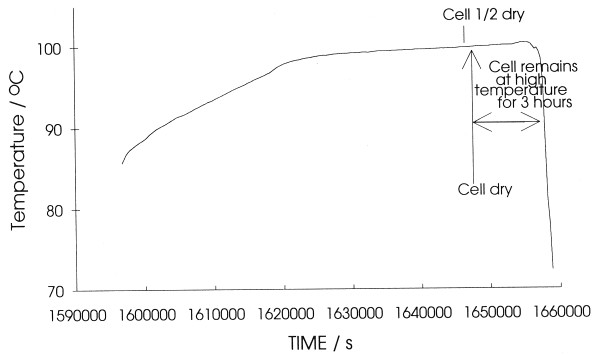
(ii) the values of the heat transfer coefficients determined in a variety of ways (see below) both with and without the calibrating resistance heater (see Fig 2 for an example of the temperature-time and cell potential-time transients) are close to those given by the product of the Stefan-Boltzmann coefficient and the radiant surface areas of the cells.
(iii) the variations of the heat transfer coefficients with time (due to the progressive fall of the level of the electrolyte) may be neglected at the first level of approximation (heat balances to within 99%) as long as the liquid level remains in the upper, silvered portions of the calorimeters.
(iv) the room temperature is controlled and set equal to that of the water baths which contain
secondary cooling circuits; this allows precise operation of the calorimeters at low to intermediate
temperatures (thermal balances can be made to within 99.9% if this is required).
(v) heat transfer from the cells becomes dominated by evaporation of D2O as the cells are driven to the boiling point.
(vi) the current efficiencies for the electrolysis of D2O (or H2O) are close to 100%.
Figure 1. Schematic diagram of the single compartment open vacuum Dewar calorimeter cells used in this work.
Figure 2. Segment of a temperature-time/cell potential-time response (with 0.250 W heat calibration pulses) for a cell containing a 12.5 × 1.5mm platinum electrode polarised in 0.IM LiOD at 0.250A.
[analysis]
Modelling of the Calorimeters
The temperature-time variations of the calorimeters have been shown to be determined by the differential equation [1]
In equation [1] the term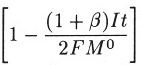 
allows for the change of the water equivalent with time;
the term β was introduced to allow for a more rapid decrease than would be given by electrolysis
alone (exposure of the solid components of the cell contents, D2O vapour carried off in the gas
stream). As expected, the effects of β on Qf and K0R can be neglected if the cells are operated below 60°C. Furthermore, significant changes in the enthalpy contents of the calorimeters are normally only observed following the refilling of the cells with D2O (to make up for losses due to electrolysis and evaporation) so that it is usually sufficient to use the approximation [2]
The term 
allows for the decrease of the radiant surface area with time but, as we have already noted, this term may be neglected for calorimeters silvered in the top portion
(however, this term is significant for measurements made in unsilvered Dewars (1); see also (7)). Similarly, the effects of conductive heat transfer are small. We have therefore set Φ = 0 and have made a small increase in the radiative heat transfer coefficient k0R to k’R to allow for this
assumption. We have shown (see Appendix 2 of (1)) that this leads to a small underestimate of Qf (t); at the same time the random errors of the estimations are decreased because the number of parameters to be determined is reduced by one.
We have also throughout used the temperature of the water bath as the reference value and
arrive at the simpler equation which we have used extensively in our work:
[analysis]
Methods of Data Evaluation: the Precision and Accuracy of the
Heat Transfer Coefficients
A very useful first guide to the behaviour of the systems can be obtained by deriving a
lower bound of the heat transfer coefficients (designated by (k’R)6 and/or (k’R)11 in our working manuals and reports) which is based on the assumption that there is zero excess enthalpy generation within the calorimeters:
[4]
The reason why (k’R)11 is a lower bound is because the inclusion of any process leading to the generation of heat within the cells (specifically the heat of absorption of D (or H) within the lattice or the generation of excess enthalpy within the electrodes) would increase the derived value of this heat transfer coefficient: (k’R)11 will be equal to the true value of the coefficient only if there is no such source of excess enthalpy in the cells as would be expected to hold, for example, for the polarisation of Pt in D2O solutions, Fig 2. The simplest procedure is to evaluate these coefficients at a set of fixed times following the addition of D2O to make up for losses due to electrolysis and/or evaporation. Convenient positions are just before the times, t1, at which the calibrating heating pulses are applied to the resistive heaters, Fig 3. For the particular experiment illustrated in Fig 2, the mean value of (k’R)11 for 19 such measurements is 0.7280 × 10-9WK-4 with a standard deviation σ(k’R)11 = 0.0013WK-4 or 0.17% of the mean.
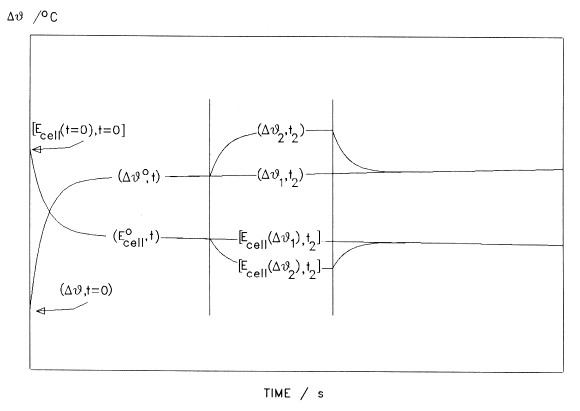
Figure 3. Schematic diagram of the methodology used for the calculations.
It is evident therefore that even such simple procedures can give precise values of the heat transfer coefficients but, needless to say, it is also necessary to investigate their accuracy. We have always done this at the next level of complication by applying heater pulses lying in the time range t1 < t < t2 and by making a thermal balance just before the termination of this pulse at t = t2. This time is chosen so that
t2 -t1 ≥ 6τ [5]
where τ is the thermal relaxation time
[6]
The scheme of the calculation is illustrated in Fig 3: we determine the temperatures and cell potentials at t2 as well as the interpolated values (Δθ1, t2) and [Ecell(Δθ1, t2) ] which would apply
at these times in the absence of the heater calibration pulse. We derive the heat transfer coefficient which we have designated as (k’R)2 using
The mean value of (k’R)2 for the set of 19 measurements is 0.7264WK-4 with a standard deviation σ(k’R)2 = 0.0099WK-4 or 1.4% of the mean.
The comparison of the means and standard deviations of (k’R)2 and (k’R)11 leads to several important conclusions:
(i) in the first place, we note that the mean of (k’R)11 is accurate as well as precise for such blank
experiments: the mean of (k’R)11 is within 0.2σ of the independently calibrated mean values of (k’R)2 ; indeed, the mean of (k’R)11 is also within ~ 1σ of the mean of (k’R)2 so that the differences between (k’R)2 and (k’R)11 are probably not significant.
(ii) as expected, the precision of (k’R)2 is lower than that of (k’R)11. This is due mainly to the fact
that (k’R)2 (and other similar values) are derived by dividing by the differences between two
comparably large quantities (θbath + Δθ2)4 – (θbath + Δθ1)4 , equation (7). The difference (θbath + Δθ)4 – (θbath)4 used in deriving (k’R)11, equation [4], is known at a higher level of precision.
(iii) the lowering of the precision of (k’R)2 as compared to that of (k’R)11 can be avoided by fitting the integrals of equation [1] (for successive cycles following the refilling of the cells) directly to the experimental data (in view of the inhomogeneity and non-linearity of this differential equation, this integration has to be carried out numerically (1) although it is also possible to apply approximate algebraic solutions at high levels of precision (8)). Since the fitting procedures use all the information contained in each single measurement cycle, the precision of the estimates of the heat transfer coefficients, designated as (k’R)5 , can exceed that of the coefficients (k’R)11. We have carried out these fitting procedures by using non-linear regression techniques (1-5) which have the advantage that they give direct estimates of σ(k’R)5 (as well as of the standard deviations of the other parameters to be fitted) for each measurement cycle rather than requiring the use of repeated cycles as in the estimates of σ(k’R)11 or σ(k’R)2. While this is not of particular importance for the estimation of k’R for the cell types illustrated in Fig 1 (since the effects of the irreproducibility of refilling the cells is small in view of the silvering of the upper portions of the Dewars) it is of much greater importance for the measurements carried out with the earlier designs (1) which were not silvered in this part; needless to say, it is important for estimating the variability of Qf for measurements with all cell designs.
Estimates of k’R have also been made by applying low pass filtering techniques (such as the Kalman filter (6) and (8)); these methods have some special advantages as compared to the application of non-linear regression analysis and these advantages will be discussed elsewhere.(8) The values of the heat transfer coefficients derived are closely similar to those of (k’R)5.
Low pass filtering and non-linear regression are two of the most detailed (and complicated) methods which we have applied in our investigation. Such methods have the special advantage that they avoid the well-known pitfalls of making point-by-point evaluations based on the direct application of the differential equation modelling the system. These methods can be applied equally to make estimates of the lower bound heat transfer coefficient, (k’R)11. However, in this case the complexity of such calculations is not justified because the precision and accuracy of (k’R)11 evaluated point-by-point is already very high for blank experiments, see (i) and (ii) above. Instead, the objective of our preliminary investigations has been to determine what information can be derived for the Pd – H2O and Pd – D2O systems using (k’R)11 evaluated point-by-point and bearing in mind the precision and accuracy for blank experiments using Pt cathodes. As we seek to illustrate this pattern of investigation, we will not discuss the methods outlined in this subsection (iii) further in this paper.
(iv) we do, however, draw attention once again to the fact that in applying the heat transfer
coefficients calibrated with the heater pulse ΔQH(t – t1) – ΔQH(t – t2) we have frequently used the coefficient defined by 
and determined at t = t2 to make thermal balances at the point just before the application of the
calibrating heater pulse, Fig 3. The differences between the application of (k’R)2 and (k’R)4 are
negligible for blank experiments which has not been understood by some authors e.g.,(9). However, for the Pd – D2O and Pd alloy – D2O systems, the corresponding rate of excess enthalpy generation, (Qf)2, is significantly larger than is (Qf)4 for fully charged electrodes. As we have always chosen to underestimate Qf, we have preferred to use (Qf)4 rather than (Qf)2.
The fact that (Qf)2 > (Qf)4 as well as other features of the experiments, shows that there is an element of “positive feedback” between the increase of temperature and the rate of generation of excess enthalpy. This topic will be discussed elsewhere (8); we note here that the existence of this feedback has been a major factor in the choice of our calorimetric method and especially in the choice of our experimental protocols. As will be shown below, these provide systems which can generate excess enthalpy at rates above 1kWcm-3.
Applications of Measurements of the Lower Bound Heat Transfer Coefficients to the Investigation of the Pd – D2Ο System
In our investigations of the Pd – D2O and Pd alloy – D2O systems we have found that a
great deal of highly diagnostic qualitative and semi-quantitative information can be rapidly obtained by examining the time-dependence of the lower bound heat transfer coefficient, (k’R)11. The qualitative information is especially useful in this regard as it provides the answer to the key question: “is there generation of excess enthalpy within (or at the surface) of Pd cathodes polarised in D2O solutions?”
We examine first of all the time-dependence of (k’R)11 in the initial time region for the
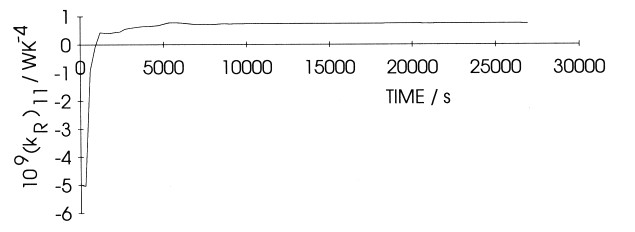
blank experiment of a Pt cathode polarised in D2O solution which has been illustrated by Fig 2. Fig 4 shows that (k’R)11 rapidly approaches the true steady state value 0.728 × 10-9WK-4 which applies to this particular cell. We conclude that there is no source of excess enthalpy for this system and note that this measurement in itself excludes the possibility of significant re-oxidation of D2 at the anode or re-reduction of O2 at the cathode.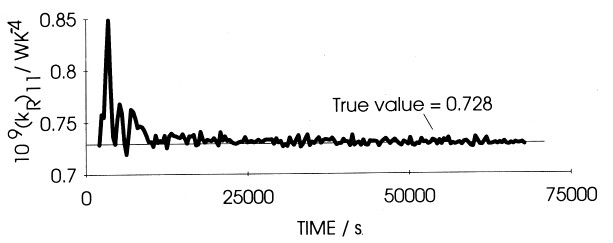
Figure 4. Plot of the heat transfer coefficient for the first day of electrolysis of the experiment described in Fig 2.
We examine next the behaviour of a Pd cathode in H2O, Fig 5. The lower bound heat transfer coefficient again approaches the true value 0.747WK-4 for the particular cell used with
increasing time but there is now a marked decrease of (k’R)11 from this value at short times. As we
have noted above, such decreases show the presence of a source of excess enthalpy in the system which evidently decreases in accord with the diffusional relaxation time of Η+ in the Pd cathode: this source can be attributed to the heat of absorption of H+ within the lattice. We also note that the measurement of (k’R)11 in the initial stages is especially sensitive to the presence of such sources of excess enthalpy because (θbath + Δθ)4 – θbath4 → 0 as t → 0, equation [4]. Furthermore, in the absence of any such source of excess enthalpy the terms [Ecell – Ethermoneutral,bath]I and CP,D2O,lM0(dΔθ/dt) will balance. The exclusion of the unknown enthalpy source must therefore give a decrease of (k’R)11 from the true value of the heat transfer coefficient. We see that this decrease is so marked for the Pd – H2O that (k’R)11 is initially negative! The measurements of (k’R)11 are highly sensitive to the exact conditions in the cell in this region of time, so that minor deviations from the true value (as for the Pt – D2O system, Fig 4) are not significant.
We observe also that measurements of (k’R)11 in the initial stages of the experiments provide an immediate answer to the vexed question: “do the electrodes charge with D+ (or H+)?” It is a common experience of research groups working in this field that some samples of Pd do not give cathodes which charge with D+ (or, at least, which do not charge satisfactorily). A library of
plots of (k’R)11 versus time is a useful tool in predicting the outcome of any given experiment!
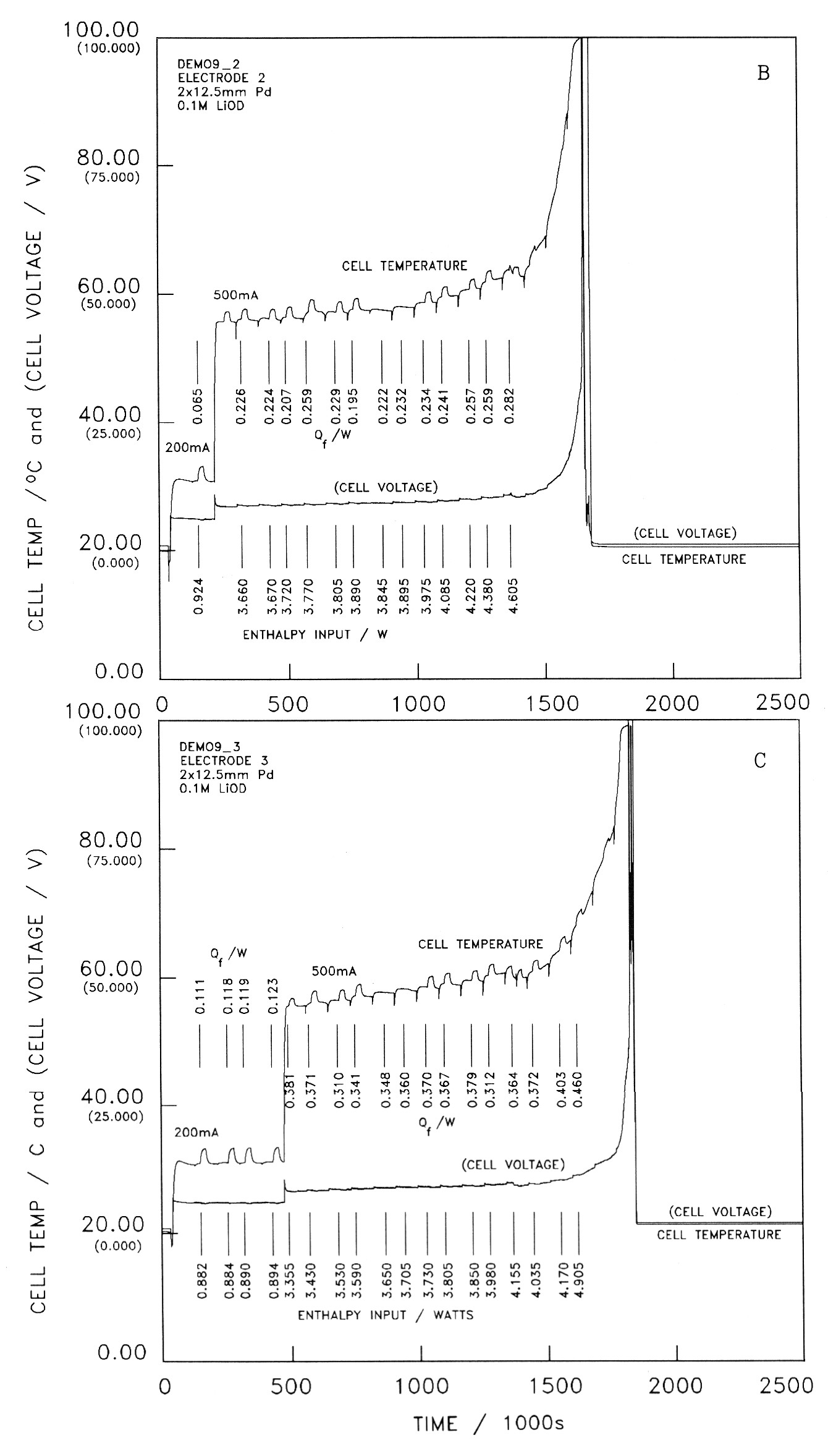
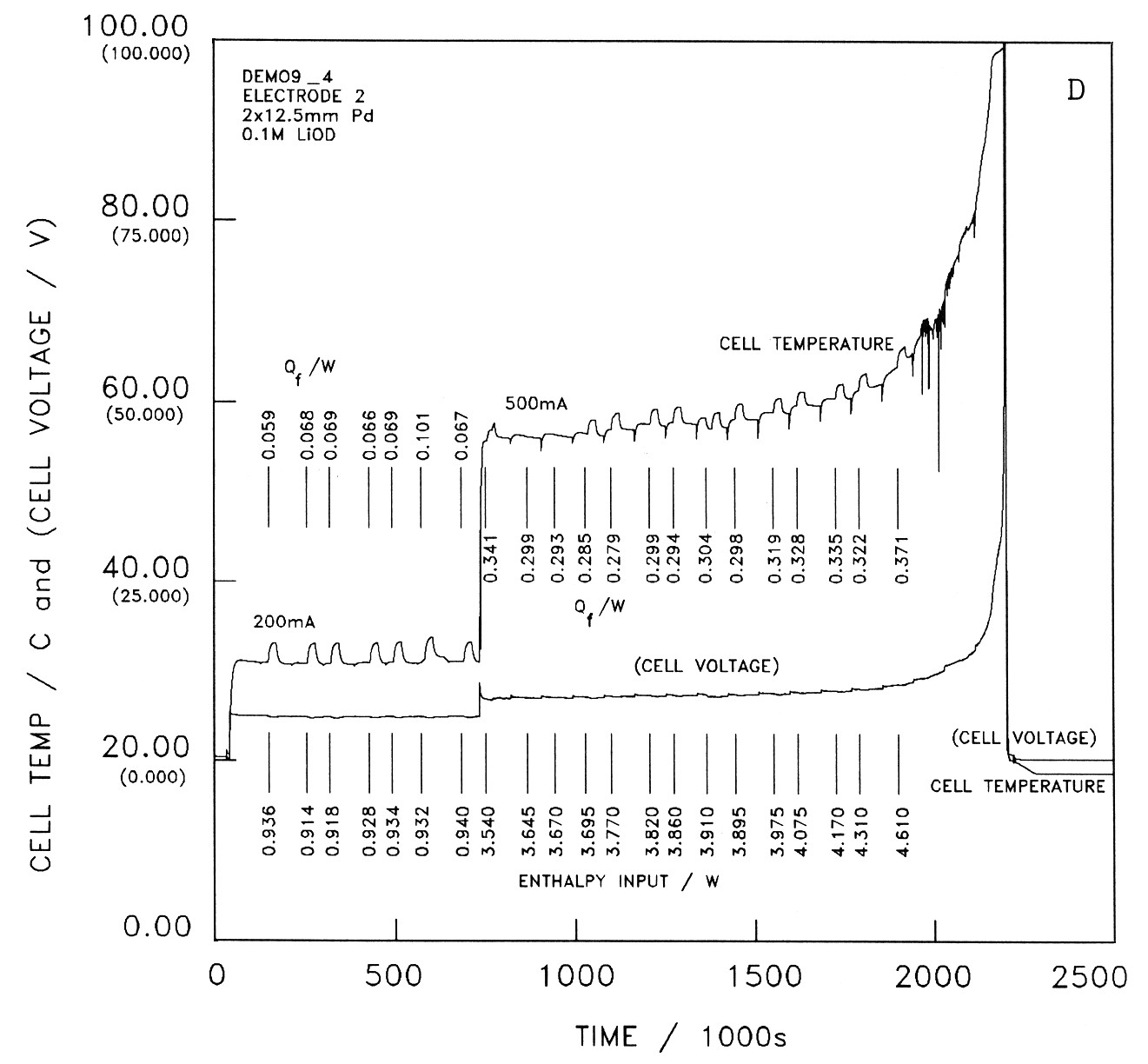
We examine next the results for one Pd cathode polarised in D2O solution out of a set of four whose behaviour we will discuss further in the next section. Fig 6B gives the overall temperature-time and cell potential-time data for the second electrode of the set. The overall objective of this part of our investigations has been to determine the conditions required to produce high rates of excess enthalpy generation at the boiling point of the D2O solutions. Our protocol for
the experiment is based on the hypothesis that the further addition of D+ to cathodes already highly loaded with deuterium will be endothermic. We therefore charge the electrodes at low to intermediate current densities and at temperatures below 50°C for prolonged periods of time; following this, the current densities are increased and the temperature is allowed to rise. The D+ is then retained in the cathodes and we take advantage of the “positive feedback” between the temperature and the rate of excess enthalpy generation to drive the cells to the boiling point, Fig 6.
Figure 5. Plot of the heat transfer coefficient for the first day of electrolysis in a “blank” cellcontaining a 12.5 × 2mm palladium electrode polarised in O.1M LiOH at 0.250mA.
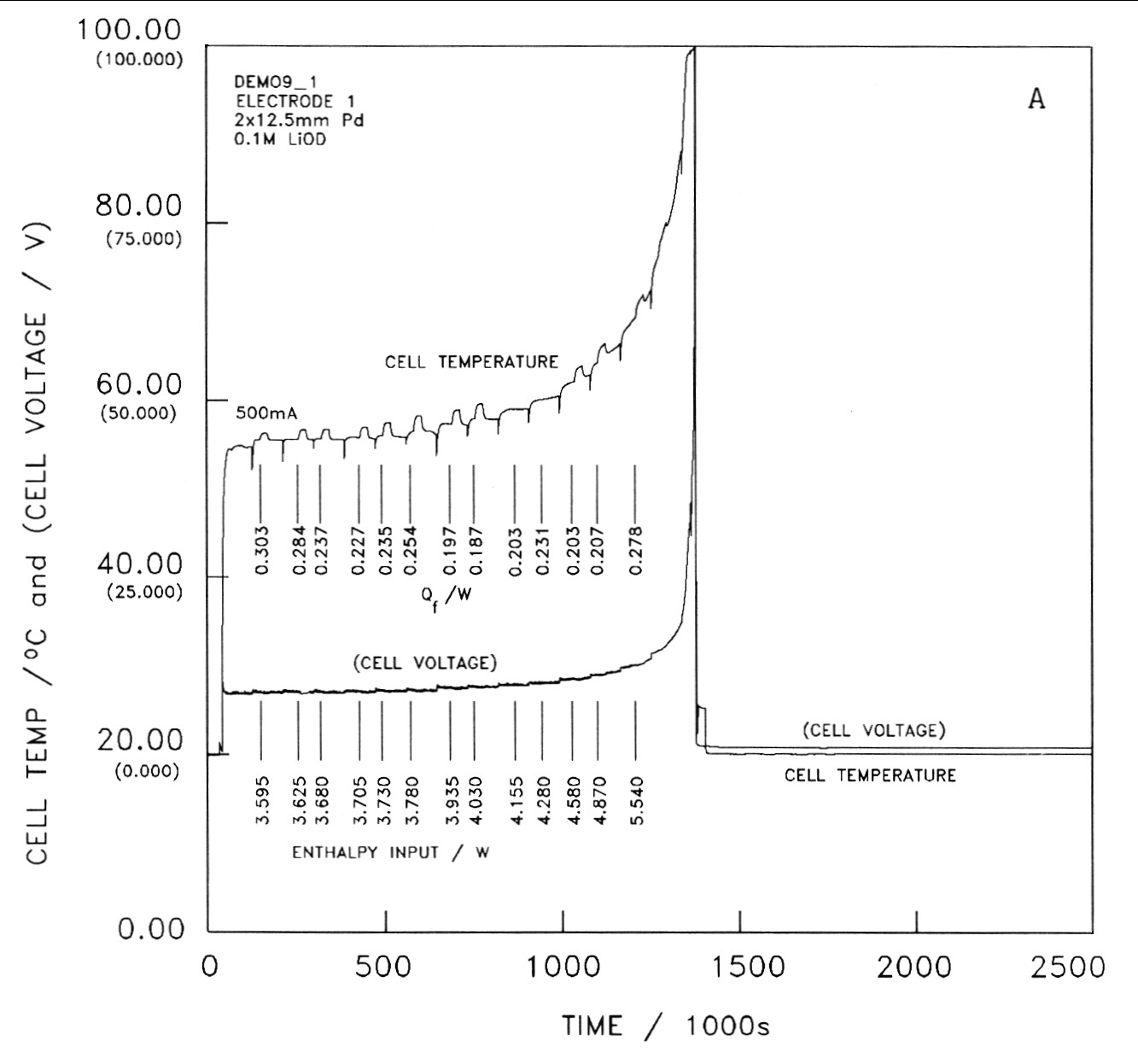
(Figure 6A)
(Figure 6D)
Figure 6. Temperature-time and potential-time profiles for four 12.5 × 2mm palladium electrodes polarised in heavy water (0.1M LiOD). Electrolysis was started at the same time for all cells. The input enthalpies and the excess enthalpy outputs at selected times are indicated on the diagrams. The current in the first cell was 0.500A. The initial current in each of the other 3 cells was 0.200A, which was increased to 0.500A at the beginning of days 3, 6, and 9, respectively.
We examine next the behaviour of the lower bound heat transfer coefficient as a function
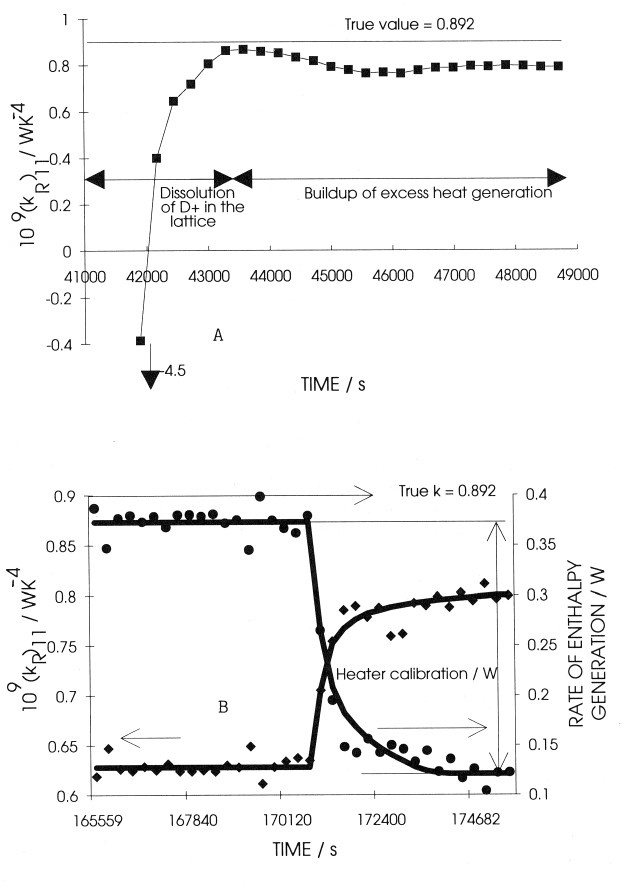
of time in three regions, Figs 7A-C. For the first day of operation, Fig 7A, (k’R)11 is initially
markedly negative in view of the heat of dissolution of D+ in the lattice. As for the case of dissolution of H+ in Pd, this phenomenon decays with the diffusional relaxation time so that
(k’R)11 increases towards the true value for this cell, 0.892 × 10-9WK-4. However, (k’R)11 never
reaches this final value because a second exothermic process develops namely, the generation of
excess enthalpy in the lattice. In view of this, (k’R)11 again decreases and we observe a maximum:
these maxima may be strongly or weakly developed depending on the experimental conditions such as the diameter of the electrodes, the current density, the true heat transfer coefficients, the level of excess enthalpy generation etc.
We take note of an extremely important observation: although (k’R)11 never reaches the true value of the heat transfer coefficient, the maximum values of this lower bound coefficient are the minimum values of k’R which must be used in evaluating the thermal balances for the cells. This maximum value is quite independent of other methods of calibration and, clearly, the use of
this value will show that there is excess enthalpy generation both at short and at long times. These estimates in Qf (which we denote by (Qf)11 are the lower bounds of the excess enthalpy. The conclusion that there is excess enthalpy generation for Pd cathodes polarised in D2O is inescapable and is independent of any method of calibration which may be adopted so as to put the study on a quantitative basis. It is worth noting that a similar observation about the significance of our data was made in the independent review which was presented at the 2nd Annual Conference on Cold Fusion. (6)
(Figure 7A, 7B)
(Figure 7C)
Figure 7. Plots of the lower bound heat transfer coefficient as a function of time for three different periods of the experiment described in Fig. 6B: (A) the first day of electrolysis, (B) during a period including the last part of the calibration cycle, and (C) the last day of electrolysis.
We comment next on the results for part of the second day of operation, Fig 7B. In the
region of the first heater calibration pulse (see Fig 6), (k’R)11 has decreased from the value shown
in Fig 7A. This is due to the operation of the term ΔQ which is not taken into account in
calculating (k’R)11, see equation [4]. As we traverse the region of the termination of the pulse ΔQ,
t=t2, (k’R)11 shows the expected increase. Fig 7B also illustrates that the use of the maximum value of (k’R)11, Fig 7A, gives a clear indication of the excess enthalpy term ΔQ, here imposed by the resistive heater. We will comment elsewhere on the time dependencies of (k’R)11 and of Q in the regions close to t = t1 and t = t2. (8)
The last day of operation is characterised by a rapid rise of temperature up to the boiling point of the electrolyte leading to a short period of intense evaporation/boiling Fig 8. The evidence for the time dependence of the cell contents during the last stages of operation is discussed in the next section. Fig 7C shows the values of (k’R)11 calculated using two assumed atmospheric pressures, 0.953 and 0.97 bars. The first value has been chosen to give a smooth evaporation of the cell contents (M0 = 5.0 D2O) i.e., no boiling during the period up to the point when the cell becomes dry, 50,735 s. However, this particular mode of operation would have required the cell to have been half-full at a time 2.3 hrs before dryness. Furthermore, the ambient pressure at that time was 0.966 bars. We believe therefore that such a mode of operation must be excluded. For the second value of the pressure, 0.97 bars, the cell would have become half empty 11 minutes before dryness, as observed from the video recordings (see the next section) and this in turn requires a period of intense boiling during the last 11 minutes. It can be seen that the heat transfer coefficient (k’R)11 decreases gradually for the assumed condition P = 0.953 bars whereas it stays more nearly constant for P = 0.97 up to the time at which the cell is half-full, followed by a very rapid fall to marked negative values. These marked negative values naturally are an expression of the high rates of enthalpy generation required to explain the rapid boiling during the last 11 minutes of operation. The true behaviour must be close to that calculated for this value of the ambient pressure.
Figure 8. Expansion of the temperature-time portion of Fig 6B during the final period of rapid boiling and evaporation.
Figs 9A and B give the rates of the specific excess enthalpy generation for the first and last day corresponding to the heat transfer coefficients, Figs 7A and C. On the first day the specific rate due to the heat of dissolution of D+ in the lattice falls rapidly in line with the decreasing rate of diffusion into the lattice coupled with the progressive saturation of the electrode. This is followed by a progressive build up of the long-time rate of excess enthalpy generation. The rates of the specific excess enthalpy generation for the last day of operation are given for the two assumed atmospheric pressures P*=0.953 and 0.97 bars in Fig 9B. These rates are initially insensitive to the choice of the value of P*. However, with increasing time, (Qf) for the first condition increases reaching ~300 watts cm-3 in the final stages. As we have noted above, this particular pattern of operation is not consistent with the ambient atmospheric pressure. The true behaviour must be close to that for P*=0.97 bars for which (Qf) remains relatively constant at ~ 20W cm-3 for the bulk of the experiment followed by a rapid rise to ~ 4kW cm-3 as the cell boils dry.
A Further Simple Method of Investigating the Thermal Balances for the Cells Operating in the Region of the Boiling Point
It will be apparent that for cells operating close to the boiling point, the derived values of
Qf and of (k’R)11 become sensitive to the values of the atmospheric pressure (broadly for θcell >
97.5°C e.g., see Fig 9B.) It is therefore necessary to develop independent means of monitoring the progressive evaporation/boiling of the D2O. The simplest procedure is to make time-lapse video recordings of the operation of the cells which can be synchronised with the temperature-time and cell potential-time data. Figs 6A-D give the records of the operation of four such cells which are illustrated by four stills taken from the video recordings, Fig 10A-D. Of these, Fig 10A illustrates the initial stages of operation as the electrodes are being charged; Fig 10B shows the first cell being driven to boiling, the remaining cells being still at low to intermediate temperatures; Fig 10C shows the last cell being driven to boiling, the first three having boiled dry; finally, 10D shows all cells boiled dry.
As it is possible to repeatedly reverse and run forward the video recordings at any stage of operation, it also becomes possible to make reasonably accurate estimates of the cell contents. We have chosen to time the evaporation/boiling of the last half of the D2O in cells of this type and this allows us to make particularly simple thermal balances for the operation in the region of the
boiling point. The enthalpy input is estimated from the cell potential-time record, the radiative
output is accurately known (temperature measurements become unnecessary!) and the major enthalpy output is due to evaporation of the D2O. We illustrate this with the behaviour of the cell, Fig 6D, Fig 10D.
Figure 9. Plots of the specific excess enthalpy generation for (A) the first and (B) the last day of
the experiment described in Fig 6B and using the heat transfer coefficients given in Figs 7A and
7C.
16
CALCULATION
Enthalpy Input
By electrolysis = (Ecell – 1.54) × Cell Current ~ 22,500J
Enthalpy Output
To Ambient ≈ k´R [(374.5°)4 – (293.15°)4] × 600s = 6,700J
In Vapour ≈ (2.5 Moles × 41KJ/Mole) = 102,500J
Enthalpy Balance
Excess Enthalpy ≈ 86,700J
Rate of Enthalpy Input
By Electrolysis, 22,500J/600s = 37.5W
Rate of Enthalpy Output
To Ambient, 6,600J/600s = 11W
In Vapour, 102,500J/600s ≈ 171W
Balance of Enthalpy Rates
Excess Rate ≈ 144.5W
Excess Specific Rate ≈ 144.5W/0.0392cm3 ≈ 3,700Wcm-3
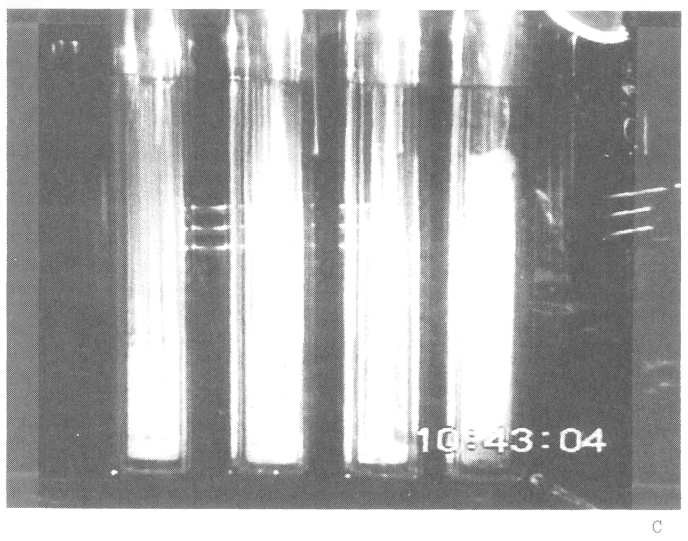
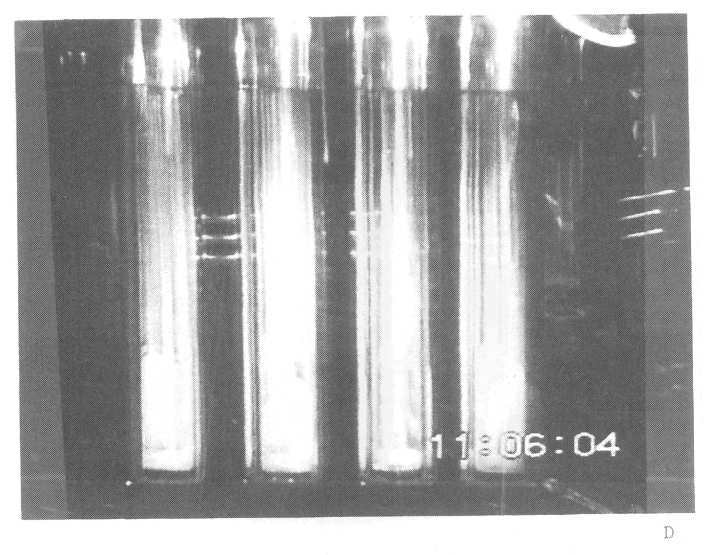
Figure 10. Stills of video recordings of the cells described in Fig 6 taken at increasing times. (A) Initial charging of the electrodes. (B) The first cell during the final period of boiling dry with the other cells at lower temperatures. (C) The last cell during the final boiling period, the other cells having boiled dry. (D) All the cells having boiled dry.
Part of a similar boil-off video can bee seen here:
http://www.youtube.com/watch?v=OMuNIedOJ90
[Abd’s note: August 12, 2017, this video is not available. The Phys Lett A publication had one image only, unintelligible, no video ref. However, these videos exist, courtesy of Steve Krivit:
Pons-Fleischmann Four-Cell Boil-Off (Pons Presentation) (Japanese overdub?)
Pons-Fleischmann Four-Cell Boil-Off (Pons Presentation) (no sound)]
We note that excess rate of energy production is about four times that of the enthalpy input even for this highly inefficient system; the specific excess rates are broadly speaking in line with those achieved in fast breeder reactors. We also draw attention to some further important features: provided satisfactory electrode materials are used, the reproducibility of the experiments is high; following the boiling to dryness and the open-circuiting of the cells, the cells nevertheless remain at high temperature for prolonged periods of time, Fig 8; furthermore the Kel-F supports of the electrodes at the base of the cells melt so that the local temperature must exceed 300ºC.
We conclude once again with some words of warning. A major cause of the rise in cell voltage is undoubtedly the gas volume between the cathode and anode as the temperature approaches the boiling point (i.e., heavy steam). The further development of this work therefore calls for the use of pressurised systems to reduce this gas volume as well as to further raise the operating temperature. Apart from the intrinsic difficulties of operating such systems it is also not at all clear whether the high levels of enthalpy generation achieved in the cells in Figs 10 are in any sense a limit or whether they would not continue to increase with more prolonged operation. At a specific excess rate of enthalpy production of 2kW cm-3, the electrodes in the cells of Fig 10
are already at the limit at which there would be a switch from nucleate to film boiling if the current flow were interrupted (we have shown in separate experiments that heat transfer rates in the range 1-10kW cm-2 can be achieved provided current flow is maintained i.e., this current flow extends the nucleate boiling regime). The possible consequences of a switch to film boiling are not clear at this stage. We have therefore chosen to work with “open” systems and to allow the cells to boil to dryness before interrupting the current.
GLOSSARY OF SYMBOLS USED
CP,O2,g Heat capacity of O2, JK-1mol-1.
CP,D2,g Heat capacity of D2, JK-1 mol-1.
CP,D2O,l Heat capacity of liquid D2O, JK-1mol-1.
CP,D2O,g Heat capacity of D2O vapour, JK-1mol-1.
Ecell Measured cell potential, V
Ecell,t=0 Measured cell potential at the time when the initial values of the parameters are evaluated, V
Ethermoneutral bath Potential equivalent of the enthalpy of reaction for the dissociation of heavy water at the bath temperature, V
F Faraday constant, 96484.56 C mol-1.
H Heaviside unity function.
I Cell current, A.
k0R Heat transfer coefficient due to radiation at a chosen time origin, WK-4
(k’R) Effective heat transfer coefficient due to radiation, WK-4 Symbol for liquid phase.
L Enthalpy of evaporation, JK–1mol-1.
M0 Heavy water equivalent of the calorimeter at a chosen time origin, mols.
P Partial pressure, Pa; product species. P* Atmospheric pressure
P* Rate of generation of excess enthalpy, W.
Qf(t) Time dependent rate of generation of excess enthalpy, W.
T Time, s.
Ν Symbol for vapour phase.
∆Q Rate of heat dissipation of calibration heater, W.
Δθ Difference in cell and bath temperature, K.
Θ Absolute temperature, K.
θbath Bath temperature, K.
Λ Slope of the change in the heat transfer coefficient with time.
Φ Proportionality constant relating conductive heat transfer to the radiative heat transfer term.
References
1. Martin Fleischmann, Stanley Pons, Mark W. Anderson, Liang Jun Li and Marvin
Hawkins, J. Electroanal. Chem., 287 (1990) 293. [copy]
2. Martin Fleischmann and Stanley Pons, Fusion Technology, 17 (1990) 669. [Britz Pons1990]
3. Stanley Pons and Martin Fleischmann, Proceedings of the First Annual Conference on Cold Fusion, Salt Lake City, Utah, U.S.A. (28-31 March, 1990). [Calorimetry of the Palladium-Deuterium Systems]
4. Stanley Pons and Martin Fleischmann in T . Bressani, E. Del Guidice and G.
Preparata (Eds), The Science of Cold Fusion: Proceedings of the II Annual Conference on Cold Fusion, Como, Italy, (29 June-4 July 1991), Vol. 33 of the Conference Proceedings, The Italian Physical Society, Bologna, (1992) 349, ISBN 887794-045-X. [The calorimetry of electrode reactions and measurements of excess enthalpy generation in the electrolysis of D2 O using Pd-based cathodes]
5. M. Fleischmann and S. Pons, J. Electroanal. Chem., 332 (1992) 33. [Britz Flei1992]
6. W. Hansen, Report to the Utah State Fusion Energy Council on the Analysis of Selected Pons-Fleischmann Calorimetric Data, in T. Bressani, E. Del Guidice and G. Preparata (Eds), The Science of Cold Fusion: Proceedings of the II Annual Conference on Cold Fusion, Como, Italy, (29 June-4 July 1991), Vol. 33 of the Conference Proceedings, The Italian Physical Society, Bologna, (1992) 491, ISBN 887794-045-X. [link]
7. D. E. Williams, D. J. S. Findlay, D. W. Craston, M. R. Sene, M. Bailey, S. Croft, B.W. Hooten, C.P. Jones, A.R.J. Kucernak, J.A. Mason and R.I. Taylor, Nature, 342 (1989) 375. [Britz Will1989]
9. R.H. Wilson, J.W. Bray, P.G. Kosky, H.B. Vakil and F.G. Will, J. Electroanal. Chem., 332 (1992) 1. [Britz Wils1992]
We dedicate this paper to the memory of our friend, Mr. Minoru Toyoda.
Review tools
Links to anchors in this document:
Page numbers, referring to lenr-canr source: 1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 17 18 19 20 21
Equations e1 e2 e3 e4 e5 e6 e7 e8
Figures f1 f2 f3 f4 f5 f6 f7 f8 f9 f10
Notes n1 n2 n3 n4 n5 n6 n7 n8 n9
Section anchors (capitalization matters), anchor word in bold:
ABSTRACT [analysis]
General Features of our Calorimetry
Modelling of the Calorimeters
Methods of Data Evaluation: the Precision and Accuracy of the Heat Transfer Coefficients
Applications of Measurements of the Lower Bound Heat Transfer Coefficients to the Investigation of the Pd – D2Ο System
A Further Simple Method of Investigating the Thermal Balances for the Cells Operating in the Region of the Boiling Point
CALCULATION
GLOSSARY OF SYMBOLS USED
References
Sections also become subpages using the same anchor word. As these are created, they will be noted in the Contents metasection above, and after the section with a smalltext link.