Subpage of Calorimetry of the PD-D2O System: from Simplicity via Complications to Simplicity.
The purpose of this subpage is to study the section named below. Comments here should be aimed toward study and learning as to what is in the Original paper. This is not a place to argue “right” and “wrong,” but to seek agreement, where possible, or to delineate unresolved issues.
Methods of Data Evaluation: the Precision and Accuracy of the
Heat Transfer Coefficients
A very useful first guide to the behaviour of the systems can be obtained by deriving a
lower bound of the heat transfer coefficients (designated by (k’R)6 and/or (k’R)11 in our working manuals and reports) which is based on the assumption that there is zero excess enthalpy generation within the calorimeters:
[4]
The reason why (k’R)11 is a lower bound is because the inclusion of any process leading to the generation of heat within the cells (specifically the heat of absorption of D (or H) within the lattice or the generation of excess enthalpy within the electrodes) would increase the derived value of this heat transfer coefficient: (k’R)11 will be equal to the true value of the coefficient only if there is no such source of excess enthalpy in the cells as would be expected to hold, for example, for the polarisation of Pt in D2O solutions, Fig 2. The simplest procedure is to evaluate these coefficients at a set of fixed times following the addition of D2O to make up for losses due to electrolysis and/or evaporation. Convenient positions are just before the times, t1, at which the calibrating heating pulses are applied to the resistive heaters, Fig 3. For the particular experiment illustrated in Fig 2, the mean value of (k’R)11 for 19 such measurements is 0.7280 × 10-9WK-4 with a standard deviation σ(k’R)11 = 0.0013WK-4 or 0.17% of the mean.
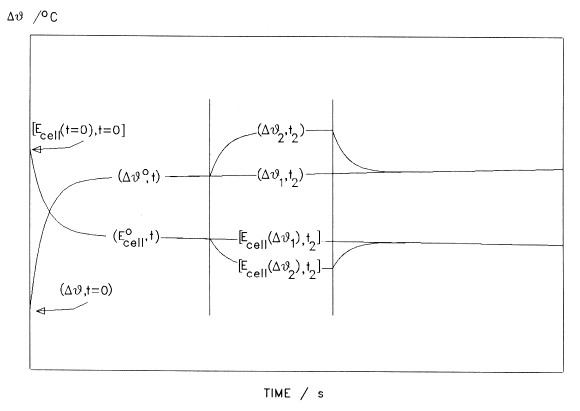
Figure 3. Schematic diagram of the methodology used for the calculations.
It is evident therefore that even such simple procedures can give precise values of the heat transfer coefficients but, needless to say, it is also necessary to investigate their accuracy. We have always done this at the next level of complication by applying heater pulses lying in the time range t1 < t < t2 and by making a thermal balance just before the termination of this pulse at t = t2. This time is chosen so that
t2 -t1 ≥ 6τ [5]
where τ is the thermal relaxation time
[6]
The scheme of the calculation is illustrated in Fig 3: we determine the temperatures and cell potentials at t2 as well as the interpolated values (Δθ1, t2) and [Ecell(Δθ1, t2) ] which would apply
at these times in the absence of the heater calibration pulse. We derive the heat transfer coefficient which we have designated as (k’R)2 using
The mean value of (k’R)2 for the set of 19 measurements is 0.7264WK-4 with a standard deviation σ(k’R)2 = 0.0099WK-4 or 1.4% of the mean.
The comparison of the means and standard deviations of (k’R)2 and (k’R)11 leads to several important conclusions:
(i) in the first place, we note that the mean of (k’R)11 is accurate as well as precise for such blank
experiments: the mean of (k’R)11 is within 0.2σ of the independently calibrated mean values of (k’R)2 ; indeed, the mean of (k’R)11 is also within ~ 1σ of the mean of (k’R)2 so that the differences between (k’R)2 and (k’R)11 are probably not significant.
(ii) as expected, the precision of (k’R)2 is lower than that of (k’R)11. This is due mainly to the fact
that (k’R)2 (and other similar values) are derived by dividing by the differences between two
comparably large quantities (θbath + Δθ2)4 – (θbath + Δθ1)4 , equation (7). The difference (θbath + Δθ)4 – (θbath)4 used in deriving (k’R)11, equation [4], is known at a higher level of precision.
(iii) the lowering of the precision of (k’R)2 as compared to that of (k’R)11 can be avoided by fitting the integrals of equation [1] (for successive cycles following the refilling of the cells) directly to the experimental data (in view of the inhomogeneity and non-linearity of this differential equation, this integration has to be carried out numerically (1) although it is also possible to apply approximate algebraic solutions at high levels of precision (8)). Since the fitting procedures use all the information contained in each single measurement cycle, the precision of the estimates of the heat transfer coefficients, designated as (k’R)5 , can exceed that of the coefficients (k’R)11. We have carried out these fitting procedures by using non-linear regression techniques (1-5) which have the advantage that they give direct estimates of σ(k’R)5 (as well as of the standard deviations of the other parameters to be fitted) for each measurement cycle rather than requiring the use of repeated cycles as in the estimates of σ(k’R)11 or σ(k’R)2. While this is not of particular importance for the estimation of k’R for the cell types illustrated in Fig 1 (since the effects of the irreproducibility of refilling the cells is small in view of the silvering of the upper portions of the Dewars) it is of much greater importance for the measurements carried out with the earlier designs (1) which were not silvered in this part; needless to say, it is important for estimating the variability of Qf for measurements with all cell designs.
Estimates of k’R have also been made by applying low pass filtering techniques (such as the Kalman filter (6) and (8)); these methods have some special advantages as compared to the application of non-linear regression analysis and these advantages will be discussed elsewhere.(8) The values of the heat transfer coefficients derived are closely similar to those of (k’R)5.
Low pass filtering and non-linear regression are two of the most detailed (and complicated) methods which we have applied in our investigation. Such methods have the special advantage that they avoid the well-known pitfalls of making point-by-point evaluations based on the direct application of the differential equation modelling the system. These methods can be applied equally to make estimates of the lower bound heat transfer coefficient, (k’R)11. However, in this case the complexity of such calculations is not justified because the precision and accuracy of (k’R)11 evaluated point-by-point is already very high for blank experiments, see (i) and (ii) above. Instead, the objective of our preliminary investigations has been to determine what information can be derived for the Pd – H2O and Pd – D2O systems using (k’R)11 evaluated point-by-point and bearing in mind the precision and accuracy for blank experiments using Pt cathodes. As we seek to illustrate this pattern of investigation, we will not discuss the methods outlined in this subsection (iii) further in this paper.
(iv) we do, however, draw attention once again to the fact that in applying the heat transfer
coefficients calibrated with the heater pulse ΔQH(t – t1) – ΔQH(t – t2) we have frequently used the coefficient defined by 
and determined at t = t2 to make thermal balances at the point just before the application of the
calibrating heater pulse, Fig 3. The differences between the application of (k’R)2 and (k’R)4 are
negligible for blank experiments which has not been understood by some authors e.g.,(9). However, for the Pd – D2O and Pd alloy – D2O systems, the corresponding rate of excess enthalpy generation, (Qf)2, is significantly larger than is (Qf)4 for fully charged electrodes. As we have always chosen to underestimate Qf, we have preferred to use (Qf)4 rather than (Qf)2.
The fact that (Qf)2 > (Qf)4 as well as other features of the experiments, shows that there is an element of “positive feedback” between the increase of temperature and the rate of generation of excess enthalpy. This topic will be discussed elsewhere (8); we note here that the existence of this feedback has been a major factor in the choice of our calorimetric method and especially in the choice of our experimental protocols. As will be shown below, these provide systems which can generate excess enthalpy at rates above 1kWcm-3.